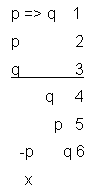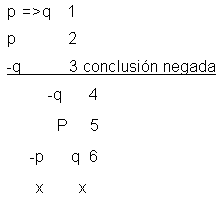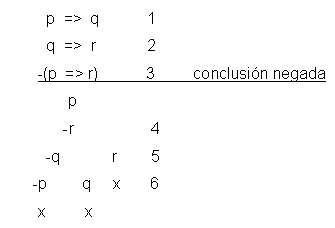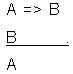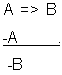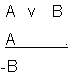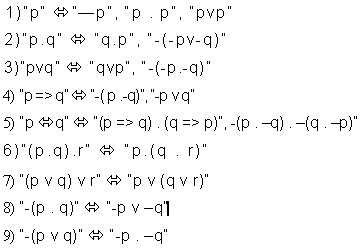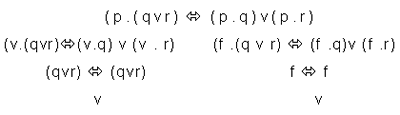Sistema de Lógica Elemental
LAS TRES DIMENSIONES DEL LENGUAJE
La semiótica estudia los lenguajes como sistemas de signos.
Estos sistemas están constituidos por un conjunto de elementos
relacionados entre sí. Los elementos son los términos
del lenguaje y las relaciones son las conexiones diversas de los
signos consigo mismos, con sus significados y con los usuarios
que se sirven de ellos para comunicarse. El filósofo Charles
Morris, teniendo en cuenta lo expuesto, definió a la semiótica
como una ciencia general de los signos y la dividió en tres
ramas: la sintaxis, la semántica y la pragmática.
La primera estudia la relación entre los signos, la segunda
la relación entre los signos y los objetos a os que se aplican
y la tercera la relación entre signos y usuarios. Cada una
de estas disciplinas tiene un campo específico de estudio.
La sintaxis se ocupa de los signos sin tener en cuenta sus significados
pero sí las relaciones entre ellos. La lógica formal
es una sintaxis que responde a reglas precisas. Estas son de dos
tipos: las de formación y las de transformación o
sustitución. Las primeras nos dicen de qué modo se
deben relacionar los signos de un determinado lenguaje lógico
y las segundas nos indican la manera de sustituir unos signos por
otros en lugares previamente determinados de una estructura sintáctica
cualquiera. Un ejemplo del primer tipo de regla puede ser la forma
en que ordenamos los sumandos de una suma. Estos deben colocarse
horizontalmente uno después del otro intercalando entre
los mismos el signo convencional que indica la operación
en cuestión: a + b + c = d. Un ejemplo del segundo tipo
de reglas es el que nos indica de qué modo podemos sustituir
una letra (variable) por otra respetando la misma estructura. Si
a = z+ y; b= z; c= y, se sustituirá "a" por su
equivalente allí donde aparezca y lo mismo sucederá con "b" y "c".
De este modo a + b + c=d se expresará una vez efectuadas
las sustituciones correspondientes: (z+ y)+z+ y= d.
La semántica tiene en cuenta los significados de los signos.
A la lógica le interesan dichos significados considerados
en su extensión, es decir, teniendo en cuenta el tipo y
la cantidad de individuos a los que puede aplicarse un signo cualquiera.
Las reglas de la semántica que indican cómo se debe
aplicar un signo a su referente o contenido significativo se denominan
reglas de asignación. Si el contenido de un signo es un
valor numérico la regla indica a que signo se le dará dicho
valor. En el ejemplo de la suma si a=4; b=l y c=7, entonces a +
b + c= d se indicará una vez sustituidas las variables por
su valores respectivos: 4+1+7= 12, siendo el resultado numérico
el valor correspondiente a “d”.
Los contenidos o significado de los signos son múltiples
y variados. Al sólo efecto de clasificar de un modo escueto
los signos según el contenido o significado que les asignemos,
vamos a considerar sólamente dos tipos de signos: denominados "términos
de propiedad" y "términos de individuo".
Los primeros son los que se aplican a conjuntos de objetos ordenados
según alguna propiedad en común. Por ejemplo, los
objetos cuya propiedad es tener cuatro patas se pueden agrupar
en el conjunto de los cuadrúpedos. 0 sea que cuando se aplica "cuadrúpedo" lo
que hacemos es aplicarlo al conjunto de objetos que nombra. Lo
mismo pasa con otras palabras. Asi la palabra "mesa" es
el nombre del conjunto de objetos cuya propiedad es "ser mesa".
Los términos de propiedad pueden hacer referencia a cualquier
propiedad, de modo que las palabras que nombran propiedades nombran
conjuntos de objetos caracterizados por dicha propiedad. Las relaciones
son
propiedades. Los parentescos son ejemplos de ellas. "Ser padre
de" expresa una relación entre por lo menos dos sujetos.
Los términos de individuo son aquellos que se aplican a
individuos. El mejor ejemplo son los nombres propios. Estos se
aplican a individuos cuando se trata de nombres de personas u objetos únicos
generalmente personalizados. "Héctor" es el nombre
de una persona. Por supuesto que muchas personas llevan ese nombre,
pero cuando usamos el nombre no lo hacemos para nombrar a todos
los Héctor sino a uno perfectamente individualizado. El
ejemplo dado no es exhaustivo, puesto que los nombres propios como
una tipología de términos aplicables a individuos
exigiria una definición de "individuo" que en
el contexto de este trabajo no daremos. También pueden considerarse
términos de individuo los sobrenombres, las descripciones
de los nombres propios, algunos pronombres personales, etc.
La pragmática estudia la relación entre los signos
y sus usuarios. Las reglas la pragmática son reglas de uso.
La expresión "buenos dias", por ejemplo, no se
usa en cualquier momento del dia. Hay una regla, tácita,
que nos indica usarla a la manana y no a la tarde o a la noche.
Lo mismo sucede con otro tipo de expresiones usadas en el lenguaje.
La retórica, concebida como una lógica de la persuasión,
en la que se tiene en cuenta a los interlocutores es, según
Morris, una pragmática. En el contexto de este trabajo ni
la retórica ni la pragmática son de interés,
en consecuencia no haremos ningún desarrollo al respecto.
|
[ Arriba
]
EL LENGUAJE
LÓGICO
Las lenguas históricas tienen
una sintaxis empírica que sirve para que quienes las
hablan puedan construir oraciones y conectarlas entre sí y
formar discursos más complejos. Estas sintaxis, propias
de lenguas como el castellano, el francés y otras semejantes,
son muy ricas en posibilidades literarias. Las ciencias en
general han usado las sintaxis de los lenguajes históricos
habida cuenta de que las distintas ciencias cultivadas por
el hombre han necesitado de esos lenguajes para transmitir
los conocimientos. Pero el uso de esos lenguajes tuvo que hacerse
con sumo cuidado porque el conocimiento científico,
entre otras condiciones, requiere de la precisión y
la exactitud a la hora de ser expresado por un sistema de signos
determinado. Es evidente que no basta con respetar la estructura
clásica de las oraciones con sujeto y predicado para
trasmitir una información cualquiera. La oración: "los
ventiladores están jugando a los dados" está bien
construida pero la información que nos brinda es nula.
Es necesario tener en cuenta los contenidos de las oraciones
para que éstas sirvan para comunicar un conocimiento.
Además, el contenido de las oraciones, o de otras expresiones
del lenguaje, depende del contenido de las palabras que se
usen para construirlas. La "oración" que dimos
como ejemplo no comunica nada precisamente porque la palabra "ventilador" y
la expresión “jugando a los dados" tienen
una denotación diferente a las que normalmente debieran
tener si con ellas se pretendiera comunicar algo usando la
sintaxis a la que hemos recurrido. Hay palabras que significan
diferentes cosas, como “llave" por ejemplo. Uno
de sus significados hace alusión a una herramienta que
se usa para desajustar tuercas, otra a un utensilio que sirve
para destrabar puertas, etc. Se les llama "homónimos" a
los términos con dichas características. Hay
palabras distintas que significan lo mismo. Por ejemplo "comprender" y "entender".
Se las
denomina "sinónimos". Este tipo de términos
que tanto en el lenguaje cotidiano como en el literario permiten
enriquecer un idioma, generalmente en el lenguaje científico
causan problemas no menores. La precisión de lenguaje
científico no permite ni la vaguedad ni la ambigüedad.
Los términos deben tener una significación
unívoca.
Los dos tipos de problemas que hemos señalado sucintamente
han preocupado a los lógicos y matemáticos
a lo largo de varios siglos. Raimundo Lulio y Leibniz propusieron
lenguajes más precisos que las lenguas históricas.
A partir de ellos tanto los lógicos como los matemáticos
se preocuparon regularmente por resolver el problema que
presentaban las imprecisiones del lenguaje científico,
principalmente en lógica y matemática. Las imprecisiones
son generalmente de dos tipos: sintácticas
y semánticas. Las paradojas reúnen estos dos tipos
de problemas. Una de las más conocidas es la de Epiménides
el cretense. Epiménides, natural de la isla de Creta, sostenía
que todos los cretenses eran mentirosos. Está claro que
si Epiménides dice la verdad, es un mentiroso puesto que
es cretense, por ende, tiene que mentir para que su aseveración
sea verdadera. Esta paradoja es una entre muchas. En el lenguaje
literario no sólo no son un problema sino, al revés,
son una ventaja. Las paradojas enriquecen el lenguaje literario.
Pero al lenguaje científico no le brindan ningun beneficio.
El teorema de Cantor
es una paradoja de la teoría de conjuntos
y se relaciona con los números cardinales. El cardinal de
un conjunto está dado por la cantidad de elementos que lo
integran. Asi el cardinal del conjunto de los meses del año
es 12, el de los días de la semana 7, etc. El teorema sostiene
que el conjunto potencia - CpS- de un conjunto cualquiera S, es
mayor que el número cardinal de S. El conjunto potencia,
CpS, de un conjunto cualquiera S, es el conjunto de todos los subconjuntos
de S incluido él mismo como subconjunto impropio, más
el conjunto vacío que no tiene elementos. Vamos mostrar
la contradicción que se genera a partir del teorema.
Llamemos T al conjunto de todos los conjuntos. Según el
teorema de Cantor el conjunto potencia de T, CpT, tiene un número
cardinal mayor que T, por lo tanto:
1) CpT>T
Considerando que T es el conjunto de todos los conjuntos, se infiere
que CpT es un subconjunto de T y por lo tanto, que todos los elementos
de CpT son elementos de T. Por ende:
2) CpT < T (lo correcto es señalar que CpT
es menor o igual a T, dado que CpT podría ser
un subconjunto impropio de T).
De este modo (1) y (2) componen la paradoja de Cantor sobre los
números cardinales. Por definición el conjunto potencia
de cualquier conjunto, en este caso el conjunto de todos los conjuntos
T, es mayor que ese conjunto ( o sea que tiene más elementos
y por lo tanto un cardinal mayor); pero al mismo tiempo T es el
conjunto de todos los conjuntos, en consecuencia CpT debe ser un
subconjunto de T (propio o impropio) y, por ende, tiene que ser
menor o a lo sumo igual que T, de no ser así o T no es el
conjunto de todos los conjuntos incluido CpT o-T es menor que CpT
y se da la paradoja de que el conjunto de todos los conjuntos es
menor a uno de sus subconjuntos, o igual si ese subconjunto es
un subconjunto impropio de T ( Se dice que un subconjunto es propio
, si es un subconjunto de un conjunto finito, cuando tiene menos
elementos que el conjunto del que forma parte, y se dice que es
impropio cuando la cantidad de elementos del subconjunto es igual
a la del
conjunto que lo contiene. Si se trata de subconjuntos de conjuntos
infinitos, el subconjunto puede tener la misma cantidad de elementos
que el conjunto que lo incluye, pero los elementos son distintos.
Todo conjunto es subconjunto de si mismo.
|
[ Arriba ]
LENGUAJE FORMAL
La necesidad de superar las paradojas
del lenguaje lógico
- matemático llevo a los estudiosos a perfeccionar dicho
lenguaje. Al principio se trató de darle a los términos
una significación unívoca, evitando de ese modo las
ambigüedades y generalidades. A los efectos de superarlas
se trató de unificar la simbología de modo tal que
no se produjesen confusiones por el uso de símbolos distintos
con referentes semejantes o el mismo símbolo con referentes
distintos. Pero como esto no fue suficiente se construyó una
sintaxis muy precisa haciendo explícitas todas las reglas
de formación y transformación que se debian usar.
La combinación entre los llamados términos primitivos
del lenguaje y las reglas sintácticas dio origen a lenguajes
formalizados muy parecidos o asociados a los cálculos aritméticos.
Los cálculos no son exactamente lenguajes porque en principio
no tienen contenido alguno. Son sintaxis puras cuyas reglas de
formación y transformación facilitan las operaciones
sin tener en cuenta los contenidos. Los lenguajes formalizados
son lenguajes porque además de la sintaxis tienen un contenido
semántico. De todos modos le deben al cálculo la
sintaxis. Esta sintaxis, más la semántica, dieron
por resultado los lenguajes formalizados que, a su vez, permitieron
presentar a la lógica como un sistema formal(l).
La adición es una estructura de este tipo y es un sistema.
Este sistema debe cumplir con ciertos requisitos: tiene que haber
un conjunto básico de n elementos y un conjunto de reglas
que regulen las relaciones entre esos elementos, de modo que un
grupo conmutativo debe constar de:
- Un conjunto K de n elementos.
- Una ley de clausura que indica que operando
con los elementos de K sólo se obtienen
elementos de K. Esta ley de composición interna define
a la operación * en un conjunto
cerrado respecto de la misma. Si el resultado de la operación
no perteneciera a K el
conjunto será abierto y la operación será externa.
- Una serie de axiomas que indican, al
funcionar como reglas, cómo operar con los
elementos de K:
A1)(a*b) = (b*a)
A2) a * (b * c) = (a * b) * c
A3) a * 0 = a A4) a * -a = 0
Usamos el signo * para indicar cualquier operación con elementos
de K definido axiomáticamente. La estructura de grupo es
una metaestructura que puede ser interpretada de distintas formas.
Si la operación indicada en el cálculo es la suma
de números naturales los elementos de K serán números
naturales. En tal caso la definición axiomática es:
A1)(a + b) = (b + a)
A2) a + (b + c) = (a + b) + c
A3)a + 0 = a A4) a + -a= 0
Si se trata de la suma de vectores la estructura de grupo permanece
inalterable y el conjunto K tendrá por elementos valores
de vectores. Esto quiere decir que cuando se suma, independientemente
de lo que se sume, siempre se lo hace respetando las reglas que
definen la estructura. En este caso dichas reglas son Al (propiedad
conmutativa), A2 (propiedad asociativa), A3 (elemento neutro),
A4 (elemento opuesto). El ejemplo dado es una estructura de cálculo.
No es un lenguaje. Un lenguaje exige asociar el cálculo
a una interpretación semántica. La lógica
formal es un lenguaje asociado a un cálculo. El cálculo
formal es un algoritmo en el que se opera sin tener en cuenta los
contenidos. No obstante se opera con ciertos símbolos y
en virtud de ciertas reglas, como lo hemos mostrado en el ejemplo.
Además el cálculo formal tiene ciertas propiedades.
Las condiciones que debe cumplir un cálculo formal (o sistema
formal) son:
- Un conjunto básico de elementos
semejantes a las palabras de un lenguaje. Este
conjunto esta constituido por los términos primitivos
del sistema. En lógica se pueden
usar símbolos para representar individuos (x, y, etc.);
propiedades (F, G, etc.);
enunciados (p, q, etc.) y también operaciones y relaciones,
por ejemplo: el producto
lógico o conjunción "."; la suma
lógica
o disyunción "v", el condicional "c"s
la
equivalencia o bicondicional "<=>", etc.
- Un conjunto de reglas de formación
que indican cómo
se deben combinar los símbolos
básicos entre sí para dar origen a estructuras
más complejas. Estas reglas nos permiten
saber cuándo las expresiones del cálculo son
correctas y pertenecen al mismo y cuándo
no lo son y esta excluidas de él.
- Un conjunto de reglas de transformación
que nos indican cómo debemos operar para
sustituir en una expresión correcta del cálculo
uno o más elementos por otros sin alterar
la estructura básica de la expresión. Una expresión
correcta es una fórmula bien
formada del sistema. Por lo tanto no toda expresión
constituye una fórmula.
Las propiedades de un cálculo formal
son:
- La consistencia, que es la imposibilidad
de poder demostrar una fórmula bien formada
verdadera y su negación. Esto se puede expresar -(A
. -A).
- La completitud, que consiste en la posibilidad
de demostrar cualquier fórmula bien
formada verdadera perteneciente al sistema.
- La decibilidad, que permite usar un procedimiento
mecánico
capaz de determinar
exhaustivamente cuándo una fórmula bien formada
pertenece al sistema.
- La satisfactibilidad, propiedad que indica
que todo cálculo
formal debe tener un modelo
en el cual las condiciones del cálculo se cumplan íntegramente.
- La independencia: los axiomas no pueden ser derivados uno de
los otros.
|
[ Arriba ]
LENGUAJE Y METALENGUAJE
Se puede mencionar a los elementos de un
lenguaje recurriendo a expresiones de ese mismo lenguaje. Esto
se debe a que los lenguajes tienen la propiedad de ser reflexivos.
Esto permite decir, por ejemplo, que 'la palabra "esdrújula" es esdrújula'.
También se puede hablar de una expresión más
compleja señalando, por ejemplo, que: "Algunos números
son primos" es una oración con sujeto y predicado.
En los dos casos se ha usado el lenguaje para hablar sobre el
lenguaje. Este procedimiento es posible porque al hablar o escribir
es posible considerar al lenguaje del que se habla o escribe
como un objeto. En tal caso el lenguaje acerca del que se habla
o escribe es un lenguaje objeto. Sus expresiones (palabras, frases,
etc.) son mencionadas. Cuando se indica que la palabra "esquema" es
de tres sílabas, se la menciona pero no se la usa. El
lenguaje desde el que se habla se denomina "metalenguaje".
Las palabras y expresiones mencionadas, por convención,
se escriben entre comillas. En el lenguaje las expresiones se
usan y no van entrecomilladas. He aquí un ejemplo:
La aritmética y la lógica
son lenguajes
En la frase anterior "aritmética" y "lógica" son
el sujeto y "son lenguajes" es el predicado. Todas las
expresiones entrecomilladas corresponden al lenguaje objeto y están
mencionadas. En la frase original que se tomó como ejemplo
son usadas.
Como la distinción entre lenguaje, metalenguaje y lenguaje
objeto es funcional y responde a un escalonamiento por niveles
se puede pasar de un nivel a otro. Si decimos "la palabra" puerta" tiene
dos sílabas" nos encontramos con tres niveles escalonados:
en el inferior, como lenguaje objeto, esta "puerta" a
la que se menciona desde la expresión metalingüística "la
palabra "puerta" tiene dos silabas". En el siguiente
nivel esta la expresión "la palabra "puerta" tiene
dos silabas" como lenguaje objeto, a la que se menciona en
la expresión metalingüística: "Si decimos "la
palabra "puerta" tiene dos sílabas" nos encontramos
con tres niveles escalonados: etc.". El escalonamiento se
remonta al infinito. Este hecho, propio de los lenguajes reflexivos,
generó problemas a veces insolubles: las paradojas. Uno
de los procedimientos par evitarlas es la distinción entre
lenguaje y metalenguaje y la convención de usar comillas
para los términos y expresiones cuando se las menciona.
La formalización de cualquier lenguaje se hace desde un
metalenguaje, puesto que formalizar un lenguaje L consiste en hacer
explfcita su estructura desde el metalenguaje L1. |
[ Arriba ]
ENUNCIADOS
YRAZONAMIENTOS
A modo de resumen introductorio de la lógica clásica
conviene recordar que los enunciados son expresiones del lenguaje
cuya característica fundamental es ser verdaderos o falsos.
Se los distingue de otras expresiones lingüísticas como
las preguntas, las órdenes, las súplicas o las exclamaciones
en tanto que ninguna de estas expresiones se caracteriza por la verdad
o falsedad. Un enunciado es verdadero cuando informa adecuadamente
y falso cuando no lo hace. Este criterio de verdad parte del supuesto
de que entre el lenguaje y lo que éste describe puede haber
una cierta correspondencia. Cuando dicha correspondencia es la adecuada
estamos ante la verdad. Cuando la correspondencia no existe o no
es estrictamente adecuada, decimos que el enunciado es falso. Hay
enunciados cuya verdad o falsedad no depende de los contenidos sino
de su forma. Serán considerados a su debido tiempo.
Esta idea de la verdad proviene de los griegos, principalmente
de Aristóteles, quien afirma que decir de lo que es que
es y de lo que no es que no es, es verdadero, y decir de lo que
es que no es y de lo que no es que es, es falso.
Los enunciados pueden describir hechos o relaciones. En el primer
caso se los denomina "sintéticos" en el segundo "analíticos".
Se dice que los enunciados sintéticos se caracterizan porque
el predicado añade información al sujeto. En el enunciado "la
puerta es roja" la propiedad "rojo" añade
información al concepto sujeto "puerta" dado que
no toda puerta es roja ni el ser rojo hace a la puerta. En el enunciado "los
cuadrados son figuras geométricas de cuatro ángulos
y cuatro lados iguales" el predicado lo único que hace
es hacer explícitas las propiedades del sujeto por medio
del análisis. No añade información.
Muchos enunciados suelen tener la forma de las oraciones con sujeto
y predicado. Se los representa S es P. Un ejemplo es: Todo hombre
es racional. El verbo "ser" es el nexo que une al sujeto
con el predicado. Estos enunciados en los que el predicado se afirma
o niega categóricamente del sujeto se denominan "categóricos".
Se los clasifica teniendo en cuenta su cantidad y su cualidad.
Por la cantidad puede ser universales o particulares y por la cualidad
afirmativos o negativos. Combinando estas característica
obtenemos los siguientes enunciados categóricos típicos:
A) Universales afirmativos: Todo S es P
E) Universales negativos: Ningún S es
P
I) Particulares afirmativos: Algún S es P
0) Particulares negativos: Algún
S no es P
Estos enunciados son los componentes de distintos tipos de razonamientos.
Los razonamientos deductivos, en los que la conclusión se
desprende necesariamente de las premisas, suelen ser de este tipo:
Todo político es estadista
Todo ciudadano es político
Luego: Todo ciudadano es estadista
Los razonamientos no son ni verdaderos ni falsos sino válidos
o no válidos. Si están bien construidos son válidos
en caso contrario no.
Los razonamientos inductivos son aquellos en los que la conclusión
se deriva de modo probable de las premisas. Un ejemplo puede ser
el siguiente:
Todas las sillas del aula A son negras
Todas las sillas del aula B son negras
Luego: es probable que las sillas del aula C también sean
negras
Y también:
Si hace calor, el agua se evapora
Hace calor
Por lo tanto el agua se evapora
|
[ Arriba ]
LOGICA DE LAS PROPOSICIONES
La lógica de las proposiciones considera a los enunciados
como unidades indivisibles, es decir que no se ocupa de analizar
la estructura interna de los mismos. Esta es la razón por
la que su simbolismo no se corresponde con el de una lógica
que parte de enunciados cuya estructura es la de las oraciones con
sujeto y predicado. Este nivel de análisis recurre a esquemas
como "S es P" para representar los enunciados. Es importante
hacer explícito el sujeto y el predicado de los enunciados,
además de hacer explícitas su cantidad y su cualidad.
Para este nivel de análisis no es lo mismo decir: "todos
los gatos son negros" que aseverar "algunos gatos son negros".
Entre otras razones porque el primero de los enunciados es universal
y el segundo particular, además de ser verdadero este último
y falso el primero.
VARIABLES PROPOSICIONALES
Si consideramos a los enunciados como unidades
indivisibles, sin importarnos ni el sujeto ni el predicado o si son
universales o particulares, podemos representarlos sin ningún problema usando sólo
una letra por cada uno. Podemos, por ejemplo, simbolizar el enunciado: " todos
los perros son animales" con la letra "p", y al enunciado: " algunos
gatos son negros" con "q". Y del mismo modo podemos
hacer con cualquier enunciado diferente de los anteriores. Si son
uno, dos, tres o más, le podemos asignar a cada uno de ellos,
siguiendo el orden alfabético de las consonantes del castellano
a partir de "p", las letras que corresponden en dicha sucesión.
Si uno de los enunciados se repite, se lo representara siempre por
la misma letra tantas veces como sea necesario. Considerado una sucesión
de enunciados como ésta: algunos gatos son negros, algunos
conejos son blancos y algunos tigres son manchados, representaremos
a "algunos gatos son negros" con "p", y a los
dos siguientes enunciados con "q" y "r" respectivamente.
Las letras que usamos para representar a los enunciados se Ilaman "variables
enunciativas" o "variables proposicionales", habida
cuenta de que "proposición" es sinónimo
de "enunciado". A los efectos de simplificar nuestro lenguaje
cuando hablemos de enunciados o proposiciones estaremos diciendo
lo mismo. Además, podemos referirnos a las variables proposicionales
como si fueran las proposiciones mismas. Esto quiere decir que podemos
referirnos a "p" como la proposición o el enunciado
p.
Las proposiciones o enunciados se pueden considerar separadas de
cualquier discurso. Por ejemplo, si decimos "la puerta es amarilla" sin
relacionar esta proposición con otra la estamos considerando
aisladamente. Podemos representarla con "p". A estas proposiciones
se las suele llamar "proposiciones atómicas". También
se las llama "proposiciones simples". Por supuesto que
las proposiciones en un discurso o texto no están, generalmente,
aisladas las unas de las otras. Están conectadas de algún
modo. Estas proposiciones se denominan "moleculares" o
complejas. Un ejemplo de estas últimas puede ser "la
puerta es amarilla y la ventana es marrón". Ambas estan
conectadas por una conjunción, en este caso la "y".
Tantos las proposiciones simples como las complejas son o bien verdaderas
o bien falsas. Esto permite establecer una relación entre
las proposiciones y la verdad o la falsedad que las caracteriza.
Se denominan "valores de verdad" a la verdad y a la falsedad
de las proposiciones. Estos valores se pueden asignar a las proposiciones
de
acuerdo a ciertos criterios. Como toda proposición, hasta
tanto no se la verifique, puede ser o verdadera o falsa, asignamos
los dos valores. Supongamos que la proposición en cuestión
es p. Le asignaremos los valores "verdad" y "falsedad" del
siguiente modo:
Si la proposición
es compleja tendremos en cuenta de que manera estan conectadas
las proposiciones simples que la componen.
|
[ Arriba ]
CONECTIVAS
LÓGICAS
Los términos que conectan a unas proposiciones
con otras se denominan "conectivas". Estas conectivas
son la conjunción,
la disyunción inclusiva, la disyunción exclusiva, el
condicional, el bicondicional, la negación conjunta y la negación
alternativa. Estas conectivas se denominan "operadores diádicos" puesto
que afectan a dos proposiciones a la vez. Si digo que "Héctor
estudia y Carlos trabaja" la conectiva es la "y"s
que incide tanto sobre una como sobre la otra. Estas conectivas se
representan por medio de símbolos convencionales. En nuestro
caso las representaremos a cada una de ellas del siguiente modo:
la conjunción (y) se representa p . q, y debe leerse "p
y q". La disyunción inclusiva (o) la representaremos
pvq que debe leerse "p o q". El condicional se representa
por p=>q, y puede leerse "p entonces q". El bicondicional
p <=> q, que se puede leer "p si y sólo si q".
Y la disyunción exclusiva pwq, que puede leerse "o bien
p o bien q". Las dos conectivas restantes se derivan de las
anteriores y se explicará su funcionamiento mas adelante.
Además de las conectivas debe considerarse un operador monádico:
la negación, que representaremos con el signo -. La negación
afecta directamente a la proposición a la que antecede. Esto
significa que si niego a p, el signo de la negación se antepondrá a
p del siguiente modo: -p, que podrá leerse "no p".
También la negación puede afectar a las proposiciones
complejas consideradas en conjunto. Por ejemplo, se puede negar a
p v q en conjunto anteponiendo la negación a un paréntesis
que encierra a p v q del siguiente modo -(p v q). La negación
afecta los valores de verdad en toda proposición, ya sea simple
o compleja. Puntualmente invierte los valores de verdad. Por lo tanto
si para:
La negación no es distributiva con respecto a ninguna conectiva.
Por lo tanto -p v -q no equivale a: -(p v q), ni -(p=>q) equivale
a: -p -> -q,etc. |
[ Arriba ]
FUNCIONES
Una función aritmética tiene dos ámbitos: el
de variabilidad y el de valores. La función es la operación
de correlatar dichos ámbitos. La expresión: f (a ,
b) = c, representa una función diádica que consta de
dos variables independientes ( a, b) y una
dependiente c. La función en cuestión puede representar
distintas operaciones aritméticas. Si se trata de la función
suma tenemos en el siguiente ejemplo: a + b = c, un ámbito
de variabilidad constituido por "a + b" y un ámbito
de valores constituido por "c". Las letra a,
b, c son variables que representan valores y el signo "+" la
operación específica. Las denominadas "variables
independientes" son aquellas
a las que se le asignan valores que a su vez, efectuada la operación,
determinan el valor de la llamada "variable dependiente".
Las variables independientes estan en el ámbito de variabilidad
y la dependiente en el de valores. Las variables ocupan lugares
en la función. En la suma a y b ocupan los lugares
que están a uno y otro lado del signo más:.........
+.... , y se denomina lugares de argumento a
dichos "espacios". Esto significa que habrá funciones
de uno, dos, tres o más lugares de argumento. La función
f (a, b) = c tiene dos lugares de argumento ocupados por las variables
a y b que representan valores. Se llama diádica a una función
con dos lugares de argumento, monádica a la de uno sólo,
triádica a la de tres y asi sucesivamente. Las fimciones
en general son n ádicas.
FUNCIONES DE VERDAD
Los enunciados o proposiciones son funciones de verdad. Esto quiere
decir que se les asignan valores de verdad y, en el caso de las
proposiciones complejas, se opera con esos valores de tal modo
que al relacionar entre sí los valores de cada proposición
simple (que forma parte de una proposición compleja) obtenemos
nuevos valores que son los que corresponden a la proposición
compleja en correspondencia con la conectiva que actúa como
operador funcional. La verdad y la falsedad se asignan a las variables
proposicionales de acuerdo a criterios preestablecidos y se denominan "tablas
de verdad". No sólo las proposiciones simples tienen
tablas de verdad. Las proposiciones complejas o moleculares tienen
sus tablas correspondsentes que dependen de la conectiva o las
conectivas que hay en ellas haciendo de nexo entre las proposiciones
simples. Vamos a mostrar las tablas de verdad de proposiciones
moleculares con dos variables y conectadas por las conectivas que
usaremos.
Consideremos, a modo de ejemplo, el caso de la conjunción.
Asi como la proposición p es verdadera o falsa, tambien
p . q considerada en conjunto es verdadera o falsa. Las otras conectivas
generan también proposiciones complejas que son verdaderas
en unos casos y falsas en otros. En tanto que funciones de verdad
diádicas las conectivas lógicas y sus respectivos
lugares de argumento se representan genéricamente f( p,
q). El ámbito de variabilidad esta integrado por los valores
asignados a cada variable y el de valores por los valores de la
conectiva obtenidos luego de correlatar entre sí los valores
de las variables. Una función diádica genérica
se expresa:
El ámbito de variabilidad está consignado con una
distribución de valores veritativos para p y q determinado
por las posibilidades de combinación de dichos valores según
el número de variables usadas. Dada una variable los valores
a asignar son dos: v, f. Si son dos las posibilidades
de combinación son cuatro:
Para p: v v f f
Para q: v f v f
Si fueran tres serían ocho y asi sucesivamente de acuerdo
a la siguiente fórmula: 2*= n, en la que "2" representa
los dos valores asignables (v , f), el signo * el número
de variables y "n" la cantidad de valores a asignar a
cada una de las mismas. Si en 2*= n, * vale 1, la función
será monádica y por lo tanto 2 elevado a 1 da 2,
con lo que serán dos lo valores asignados. Si la función
es diádica 2* será 2 elevado al cuadrado y los valores
asignados serán cuatro. En el caso de una función
triádica * vale 3, y 2 se eleva a la tercera, con lo que
2x2x2 = 8. Una función triádica:
| f (p. q. r) |
| v |
v |
v |
| f |
v |
v |
| v |
f |
v |
| f |
f |
v |
| v |
v |
f |
| f |
v |
f |
| v |
f |
f |
| f |
f |
f |
tiene 8 valores por cada variable.
Veamos ahora cada una de las funciones de verdad diádicas,
que no son otras que las
conectivas lógicas.
|
[ Arriba ]
LA CONJUNCIÓN es
verdadera cuando las proposiciones que la componen son ambas
verdaderas, y falsas en los demás casos. Su tabla de verdad
es la siguiente:
| p . q |
| v |
v |
v |
| v |
f |
f |
| f |
f |
v |
| f |
f |
f |
LA DISYUNCIÓN INCLUSIVA es
verdadera en todos los casos, salvo cuando las proposiciones
simples que la componen son ambas falsas. Esto es:
| p |
v |
q |
| V |
V |
V |
| V |
V |
f |
| f |
V |
V |
| f |
f |
f |
EL CONDICIONAL es verdadero
en todos los casos salvo cuando el antecedente es verdadero y
el consecuente falso. Esto es:
p=> q
La fórmula q => p es la conversa de p => q, mientras
que la fórmula -p => -q es el inverso y la fórmula
-q => -p es la contrapositiva de p=>q.
LA IMPLICACIÓN es la validez del condicional,
es decir, un condicional verdadero en todos los casos. Un ejemplo
simple sería:
que puede leerse p implica q.
Si se emplean variables metalógicas, o sea que sustituyan
a cualesquiera fórmula del lenguaje lógico, se puede
decir que P implica lógicamente a Q siempre que P => Q
sea una tautología. Sean P y Q variables metalógicas
y que para el caso P represente "(-p v q). p" y Q represente "p",
entonces la fórmula:
"((-p v q) . p)
=>q" |
| f |
V |
V |
V |
V |
V |
V |
| f |
f |
f |
f |
V |
V |
f |
| V |
V |
V |
f |
f |
V |
V |
| V |
V |
f |
f |
f |
V |
f |
es una implicación. Ahora bien, las variables metalógicas
P y Q representan enunciados no hechos. Por lo tanto la implicación
es una relación formal entre nombre de enunciados y no entre
hechos. El condicional, en cambio, describe relaciones entre hechos
y por ese motivo no siempre ni en todos los casos debe ser verdadero.
EL BICONDICIONAL es verdadero
cuando los valores de verdad de cada proposición son equivalentes.
Este es un caso:
p<=> q |
| V |
V |
V |
| V |
f |
f |
| f |
f |
V |
| f |
V |
f |
Podemos definir a la doble implicación como la validez del
bicondicional o sea cuando este es verdadero en todos los casos.
Asi p <=> p esuna doble implicación o también
una equivalencia. |
[ Arriba ]
LA DISYUNCION EXCLUSIVA es verdadera
cuando los valores de las proposiciones conectadas son diferentes.
Por ejemplo:
| p w q |
| v |
f |
v |
| v |
v |
f |
| f |
v |
v |
| f |
f |
f |
LA NEGACIÓN CONJUNTA es una derivación
de -p . -q y se puede representar del siguiente modo: p
^ q, que se lee "ni p ni q" y que es falsa en todos
los casos salvo cuando las
proposiciones conectadas son falsas:

esta conectiva permite expresar
cualquier fórmula bien
formada del sistema sin usar la
negación ya que -p <=> p^p.
LA NEGACIÓN
ALTERNATIVA es una derivación
de -p v -q y se la representa: p/q, que es verdadera en todos los
casos salvo cuando, en el caso del ejemplo, p y q son verdaderas:
| - p v –q |
<=> |
p / q |
| f |
f |
f |
|
v |
f |
v |
| f |
v |
v |
|
v |
v |
f |
| v |
v |
v |
|
f |
v |
v |
| v |
v |
v |
|
f |
v |
f |
Utilizando una, dos o más
conectivas y una, dos o
más variables proposicionales podemos construir proposiciones
moleculares de diferente grado de complejidad. Por ejemplo, una
en la que se usen p, q, r y las conectivas => (condicional),
v (disyunción inclusiva) como la siguiente: (p => q)
v r que puede leerse "si p entonces q o r". En este caso
se nan usado parentesis para agrupar las variables de acuerdo a
un criterio arbitrario, lo que significa que se podrían
haber agrupado de otro modo. Por ejemplo: p => ( q
v r). Los paréntesis, los corchetes y las llaves son signos
de puntuación, o sea que la única función
que cumplen es la de separar y agrupar proposiciones tanto simples
como complejas. El uso de dichos signos no sólo modifica
la lectura que hacemos de las proposiciones sino también
sus tablas de verdad. En los ejemplos anteriores no sólo
las lecturas de las fórmulas son diferentes sino también
la distribución final de sus valores veritativos.
|
[ Arriba ]
MÉTODO
DE LAS TABLAS DE VERDAD
Las tablas de verdad son un método de decisión que
permite
determinar si una fórmula es verdadera o falsa. Al aplicarlo
a las funciones de verdad se mostró en qué casos una
determinada conectiva era verdadera o falsa. Se pueden hacer fórmulas
usando varias conectivas y usar las tablas de verdad para saber en
qué casos dichas fórmulas son verdaderas y en qué casos
no lo son.
Por ejemplo:
(p=>-q) . p |
| v |
f |
f |
f |
v |
| v |
v |
v |
v |
v |
| f |
v |
f |
f |
f |
| f |
v |
v |
f |
f |
es verdadera sólo en la segunda linea, o sea , cuando tanto
p =>-q como p son verdaderas, dado que el conector principal
es la conjunción. Lo mismo se puede hacer con cualquier
fórmula bien formada independientemente de su grado de complejidad,
ya sea por la cantidad de variables usadas en ella o por la reiteración
de una o más variables unidas por diferentes conectivas.
El siguiente es un ejemplo de ello:
(p . q) => ((p => r) w –q) |
v |
v |
v |
v |
v |
v |
v |
v |
f |
v |
f |
f |
v |
v |
v |
v |
f |
v |
f |
f |
v |
v |
f |
v |
v |
v |
f |
f |
f |
f |
v |
f |
v |
v |
f |
v |
v |
v |
v |
f |
v |
f |
f |
f |
f |
v |
f |
f |
v |
v |
f |
f |
v |
v |
f |
f |
v |
v |
f |
v |
f |
v |
f |
f |
f |
f |
v |
f |
v |
f |
f |
v |
MÉTODO DE DECISIÓN POR ASIGNACIÓN
DE VALORES
Existen varios métodos para decidir si una fórmula
cualquiera pertenece o no un sistema lógico, y, dado que
sólo las tautologías pertenecen al mismo, bastaría
con disponer de un procedimiento para averiguar si una fórmula
cualesquiera lo es o no lo es. Uno de ellos es el de las tablas
de verdad y otro, derivado del anterior, es el método por
asignación de valores. Este método es más
rápido pero no más efectivo que las tablas y se aplica
a partir de ciertas reglas que indican el funcionamiento de las
distintas conectivas. Considerando que los valores veritativos
son "v" y "f" se los puede asignar en una fórmula
cualquiera a todas sus variables, como en el caso de las tablas
de verdad, o a una de las variables de la fórmula elegida
arbitrariamente. El procedimiento consiste en sustituir a la variable
por el valor a asignar allí donde aparezca. El valor elegido
puede ser “f” o "v" y conviene asignarlo,
en una fórmula compleja, a la variable que más se
repita. Sea la fórmula: p => (-q . p), en cuyo caso sustituimos
la variable más repetida por "f', con lo que obtenemos
f -> ( -q . f). Una vez asignado el valor se procede
a operar según cual sea la conectiva - o conectivas- que
oficia de nexo. En el ejemplo lo que se comprueba es que la fórmula
en cuestión, cuando a la variable más repetida se
le asigna "f", el resultado es "v". Esto se
debe a que en un condicional cuando el antecedente es falso el
condicional es siempre verdadero. Si a la misma variable se le
asignase "v" el resultado es "v" o "f",
dado que en un condicional cuando el antecedente es verdadero el
condicional puede ser verdadero o falso. Ademas el consecuente
es una conjunción, que es falsa cuando una de sus variables
es falsa, pero puede ser verdadera o falsa cuando una variables
es verdadera, como es el caso. El procedimiento del ejemplo responde
a reglas. Estas reglas indican el comportamiento de las conectivas
y la negación. A los efectos de hacer claras las reglas
el signo "=" se leerá "igual a" y
el signo " <=> " será el de bicondicional.
Al operar se tendrá en cuenta que:
-
La negación invierte el valor asignado,
de modo que si p = f, -p = v, y viceversa.
-
La conjunción es "f' cuando una de sus variables
es "f “, y v o f cuando una de ellas es
v,
-
La disyunción es "v" cuando una de sus variables
es "v", y v o f cuando una de ellas es
f.
-
El condicional es siempre "v" cuando el consecuente
es "v" y cuando el antecedente es
”f”. Cuando el antecedente es "v" se lo
elimina dejando al consecuente, y se elimina el
consecuente cuando es "f' dejando el antecedente.
-
El bicondicional es verdadero cuando los valores del antecedente
y el consecuente son
iguales. Cuando en el bicondicional aparece "v" en
uno de sus componentes se la
suprime: "v <=> v = v"; "v <=> f" y "f <=> v" equivalen
a “f”.
-
Si en el bicondicional aparece "f'
se la elimina cambiando el valor de la otra
componente: "f<=>f = v"; "f<=> v
= f;v<=> f= f.
-
Por idempotencia la conjunción y la disyunción
se simplifican cuando aparecen en la
misma fórmula dos o más veces: p.p.p = p; p v
p v p = p.
Como el método tiene por fmalidad determinar si una fórmula
cualquiera es o no una tautología se habrá conseguido
el objetivo cuando se compruebe que al menos en un caso la fórmula
en cuestión es falsa y el procedimiento se detendrá de
modo inmediato. Si luego de sustituir la variable más repetida
por uno de sus valores se llega al resultado “v”,
se le asignará el otro valor “f'” hasta terminar
con el procedimiento. Esto es necesario porque puede darse el caso
de una fórmula en la que siendo “f” el valor
asignado a la variable más repetida de por resultado "v",
pero resta por saber si asignando a dicha variable el valor "v",
el resultado será el mismo. Si queda parte de la fórmula
inicial sin resolver se elige la variable que más se repite
en dicha parte - o una de las variables en el caso de que ninguna
se repita más que otra- y se continúa con el procedimiento
hasta terminar con "v" o "f' o en una variable.
Téngase en cuenta que la variable más repetida una
vez asignados los valores puede desaparecer de la fórmula
inicial, pero ello no implica que parte de dicha fórmula
sea a la vez una fórmula que debe ser testeada. Sea la fórmula:
(pv-p)=>((q=>(p.r))
Si se asigna a la variable más repetida “f” se
obtiene por sustitución:
(fw)=>((q=>(f.r))
operando se obtiene: "v", para el antecedente del condicional
principal por regla 3 y q => f,
para el consecuente de dicho condicional, ya que en (f . r) se
aplica la regla 2 de la conjunción que dice que siendo falsa
cualquiera de las variables el resultado es f. Sabemos, por la
regla del condicional que cuando el antecedente es verdadero el
condicional puede ser verdadero o falso, y que, siendo falso el
consecuente sucede exactamente lo mismo. Ya en este paso del procedimiento
se sabe que la fórmula en cuestión no es una tautología
dado que al menos en un caso es falsa. Téngase en cuenta
que q => f, es v o f (o sea q), ya que sustituida q por f, da
f=>f que es "v", y sustituida por v, da v => f
que es “f”
Sea la fórmula:
((p
. r) v (p=>q)) . (-p v q)
Se sustituye en
la misma a “p” por “f”:
((f . r) v (f =>q))
. (v v q)
Y dado que (f . r = f) y (f =>q = v) y (v v q = v)
Se obtiene: (f v v) . v
Si se sustituye a “p” por “v”:
((v . r) v (v => q )9 . (f v q)
Y dado que (v . r =r) y (v => q = q) y (f v q = q)
Se obtiene: (r v q) . q
Y sustituyendo a “q” por “f” se
obtiene:
(r v f) . f que da f
Lo que indica que la fórmula no es una tautología.
|
[ Arriba ]
LA DEFINICION
Definir es un procedimiento por medio del cual se determina el significado
de los términos de un lenguaje. Son de distinto tipo y
se las puede clasificar a partir de criterios sintácticos,
semánticos o pragmáticos. Las definiciones recursivas, por
equivalencia y axiomáticas, son sintácticas y serán
las más utilizadas en este texto.
Definiendum y definiens
Las definiciones constan de un término a definir, llamado "definendum",
y un término o expresión que define llamado "definiens".
La definición es la relación de igualdad entre el definiendum
y el definiens. Si definimos un cuadrado como un rectángulo de cuatro
lados iguales, el término "cuadrado" es el definiendum y
la expresión "rectángulo de cuatro lados iguales" es
el definiens. Por regla general el definiendum nunca debe figurar en el definiens.
En las definiciones implícitas sin embargo, pueden figurar en el definiendum
y en el definiens los mismos términos, aunque los mismos no son los
términos a definir. Es lo que sucede, verbigracia, en las definiciones
por equivalencia, en las recursivas y en las axiomáticas. Estos tres
tipos de definiciones se usan para definir los términos primitivos y
fórmulas bien formadas de los sistemas lógicos.
DEFINICIONES RECURSIVAS
Una secuencia no ordenada de variables
y conectivas no constituye una fórmula. Para hacer una fórmula de la lógica
proposicional es necesario mostrar el modo de construirlas.
Se denominan definiciones recursivas a aquellas definiciones que
nos indican cuándo estamos ante una fórmula
lógica bien formada y no sólo ante una secuencia
de símbolos lógicos. En las definiciones recursivas
se enuncian un serie de reglas que nos dicen cómo y cuáles
son las fórmulas bien formadas. Veamos una definición
recursiva en la cual se indican como son las fórmulas de
las proposiciones atómicas, de la negación y de las
proposiciones moleculares donde la conectiva utilizada es la conjunción.
Regla 1: p, q, r, etc. son fórmulas atómicas bien
formadas.
Regla 2: si p es una f. b. f entonces
-p es una fórmula
bien formada.
Regla 3: si p, q, etc., son f. b.
f entonces p v q es una fórmula
molecular bien formada
Regla 4: Sólo son fórmulas
bien formadas las definidas por estas reglas y las de ellas derivadas.
Del mismo modo se pueden definir las otras conectivas. Mas con
solo una conectiva y la negación (si no se usa la negación
conjunta o la alternativa)) es suficiente para definir a todos
los términos lógicos del sistema. Las definiciones
por equivalencia permiten hacerlo. Esto hace supérfluas
a todas las conectivas salvo a aquélla de la que no se puede
prescindir dado que se la necesita para definir a todas las otras.
DEFINICIONES POR EQUIVALENCIA
Además de las definiciones por recursividad hay definiciones
por equivalencia que, como se ha señalado, hacen posible
definir todas las conectivas a partir de una de ellas. Dado que
hemos definido la disyunción inclusiva podemos partir de
ella para definir las otras conectivas a usarse en el sistema estableciendo
las equivalencias correspondientes. La abreviatura df. significa "definición" y
=df. debe leerse: equivalente por definición.
La conjunción: (p . q) 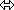 df. -( -p v -q) df. -( -p v -q)
El condicional: (p -> q) 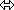 df. - p v q df. - p v q
El bicondicional: (p 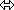 q) q) 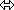 df.((
p=>q)
. (q=>p)) df.((
p=>q)
. (q=>p)) 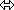 df -(-(-p v q) v (-q v p)) df -(-(-p v q) v (-q v p))
Las definiciones recursivas y por equivalencia nos permiten integrar
todas las conectivas a un sistema lógico. Estos sistemas
cuentan con un vocabulario mínimo, axiomas, reglas de formación
y de transformación. No está de más reiterar
que las primeras nos indican como ordenar las variables y las conectivas
y las segundas como se debe sustituir en una fórmula cualquiera
una variable por otra variable o por otra fórmula. Por ejemplo,
se puede sustituir en la fórmula (pwq).p la variable p por
la fórmula molecular p=>q , poniendo p=>q allí donde
aparece p. La fórmula resultante seria:
((p=>q) w q) . (p=>q)) |
[ Arriba ]
DEFINICIONES AXIOMATICAS
Las definiciones axiomáticas son aquellas en cuyo
definiens se hacen explícitos los axiomas de la operación
o el sistema que se quiere definir. La axiomática de los números
naturales de Peano es un sistema definido a partir de tres términos
primitivos: "cero", "ser sucesor de" y "número
natural". Los axiomas que forman parte del definiens son:
A1) 0 es un número natural
A2) Todo número natural tiene un sucesor
A3) 0 no es el sucesor de ningún número natural
A4) Si los numeros x e y tienen el mismo sucesor entonces x=y
A5) Siendo 0 un elemento del conjunto K y si para cada elemento x
de K existe un x' que
es su sucesor y que también pertenece a K, entonces K es el
conjunto de todos los números
naturales.
El sistema P.M de lógica de enunciados esta definido a partir
de los primitivos "-", "=>" y
"v" y por los siguientes axiomas:
A1) (pvp)=>p
A2) p => (p v q)
A3) (p v q) => (q v p) A4)(p=>q)=>((rvp)=>(rvq))
LEYES LÓGICAS
Las leyes o principios lógicos son proposiciones verdaderas
en virtud de su forma. No son los contenidos de dichas proposiciones
los que determina su verdad sino la ordenación de sus variables
y conectivas de acuerdo a ciertas formas fijas. Estas proposiciones
que son verdaderas siempre se denominan "tautologías".
Las proposiciones que hemos visto hasta ahora eran o verdaderas o
falsas y como su verdad y falsedad depende en cierta medida de los
hechos que describen se las llama "contingencias". Asi
p.q o -pvq son contingencias. En cambio una formula como p óp
es una tautología, puesto que es verdadera en todos los casos
y su verdad depende de su forma y no de los hechos. Si hacemos su
tabla de verdad tendremos;
p
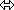 p p |
| v |
v |
v |
| f |
v |
v |
p=p es una equivalencia y se lee p equivale p o también p
es idéntica a p. Es una ley lógica y una de las expresiones
del principio de identidad. Además de este principio hay otros.
Los más conocidos son el de no contradicción y el del
tercero excluido, que los hemos visto en otros capítulos.
Enumeraremos a continuación algunas leyes lógicas
de uso frecuente.
- Principio de identidad: p
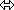 p p
- Principio de no contradicción:
-(p.-p)
- Principio del tercero excluido: (pv-p)
- Doble negación: p
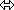 -
- p -
- p
- Idempotencia de la conjunción: p
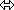 (p
. p) (p
. p)
- Idempotencia de la disyuncion: p
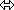 (p
v p) (p
v p)
- Ley de De Morgan para la conjunción:
p . q
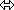 -(-pv-q) -(-pv-q)
- Ley de De Morgan para la disyunción:
pvq
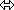 -(-p
.-q) -(-p
.-q)
- Modus ponendo ponens: ((p =>q) . p)=>q
- Modus tollendo tollens: ((p =>q) .-q)=>-p
- Modus ponendo tollens: ((pwq) . p)=> -q
- Modus tollendo ponens. ((pvq). -p)=> q
- Ley conmutativa par la conjunción:
(p . q)
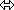 (q
- p) (q
- p)
- Ley conmutativa para la disyuncion inclusiva:
(pvq)
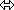 (qvp) (qvp)
- Ley asociativa para la conjuncion: (p
. (q . r))
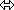 ((p
. q). r) ((p
. q). r)
- Ley asociativa para la disyuncion in.:
(p v ( q v r))
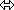 ((p
v q) v r) ((p
v q) v r)
Las leyes lógicas negadas son proposiciones contradictorias. Son lo
opuesto a la tautología, por ende la negación de
cualquier tautología da por resultado una contradicción.
Si niego, verbigracia, el principio de identidad incurro en una
contradicción:
-( p p) p) |
| f |
v |
v |
v |
| f |
f |
v |
f |
Tanto las tautologías como las contradicciones son verdaderas
o falsas respectivamente en cualquier caso de sustitución.
Esto quiere decir que, independientemente de las variables que
se usen, las fórmulas tautológicas o contradictorias
siempre serán verdaderas las primeras y falsas las segundas.
Por eso si en vez de usar p y q para expresar el Modus ponendo
ponens usamos pwq por p, y r por q tendremos:
((pwq)=> r) . (pwq)) => r
que es una tautología.
Esto es extensible a cualquier caso y vale, aunque en sentido inverso,
para las contradicciones. |
[ Arriba ]
INTERPRETACION
Las fórmulas lógicas pueden ser interpretadas, es decir,
sustituir sus variables y conectivas por enunciados y términos
de nuestra lengua. La fórmula p => -q puede interpretarse
del siguiente modo:
p: Héctor está de vacaciones -q : Héctor no
estudia
por lo cual p=>-q queda: Si Héctor está de vacaciones
entonces no estudia
La fórmula p . q . -r se puede interpretar:
Carlos estudia y Marta trabaja y Héctor no está ocupado
En esta interpretación p, q y -r simbolizan tres enunciados
en los que tanto los sujetos como los predicados son distintos. Pero
podría simbolizar una oración compleja como:
Carlos estudia, trabaja y no está ocupado
Esto se debe a que la oración compleja está integrada
por tres oraciones en las que siendo diferente cada predicado el
sujeto es el mismo. "Carlos estudia" es p, "Carlos
trabaja" es q, y "Carlos no está ocupado" es
-r.
Consideremos ahora el siguiente ejemplo:
Carlos y Marta estudian
En este caso se trata de una oración compleja con diferentes
sujetos y el mismo predicado que encierra dos proposiciones:
Carlos estudia y Marta estudia
ABSTRACCION
De los enunciados expresados en nuestra lengua, u otras, pueden abstraerse
sus formas lógicas. Estas se expresan por medio de las fórmulas
de la lógica proposicional. Como procedimiento es inverso
al de interpretación y consiste en sustituir cada enunciado
del lenguaje empírico por una fórmula atómica
o compleja del lenguaje formal. Por ejemplo, el enunciado "la
pared es blanca y la puerta está cerrada" se puede expresar
en el lenguaje abstracto de la lógica por la fórmula:
p . q
El enunciado " O bien
vamos al cine o bien estudiados " tiene
la fórmula: pwq.
La complejidad del lenguaje coloquial, así como la del científico,
varía gradualmente. La
proposición:
Si Argentina hace valer sus derechos en el caso de las papeleras
y Uruguay reconoce el peligro de contaminación que su actividad
im-plica, entonces ambos países Ilegarán a un acuerdo.
Pero si Uruguay no reconoce el peligro de la contaminación
no habrá acuerdo.
Tiene la fórmula: ((p . q) => r) .-q) => -r, o también:
((p . q)=> r) . (-q => -r)
VALIDADACIÓN
DE ARGUMENTOS POR ANALOGÍA LÓGICA
Los
argumentos pueden ser validados de diferentes maneras. En la lógica proposicional o de enunciados existen procedimientos
que permiten distinguir a los argumentos válidos de los que
no lo son. Uno de esos procedimientos es el de la analogía
lógica. Consiste en comparar cualquier argumento con una forma
metalógica que se deriva de una tautología. Estas formas
paradigmáticas son reglas lógicas, que no son otra
cosa que las leyes lógicas usadas como esquemas con los que
se comparan los argumentos. Si estos coinciden en su forma con las
de la regla se dice que el argumento es válido, de no ser
asi estara probada su invalidez.
A partir de las leyes lógicas que conocemos podemos derivar
algunas reglas. Estas se expresan por medio de variables metalógicas
que pueden ser sustituidas por fórmulas lógicas de
cualquier grado de complejidad. Las variables metalógicas
se representan por letras mayúsculas del alfabeto a partir
de A.
Un ejemplo de regla lógica es la que se deriva de la ley llamada
modus ponendo pones. La fórmula de esta ley es la siguiente:
((p =>q) => q
en esta fórmula afirmando el antecedente p se concluye válidamente
el consecuente q. La regla correspondiente es:
A => B
A_____
B
Como se ve, en la regla alguna de las conectivas desaparece y en
su lugar se ponen en columnas las formas metalógicas derivadas
de las lógicas, sustituyendo la conjunción por el ordenamiento
en columnas, poniendo a una forma debajo de la otra, y al condicional
por una línea que separa las premisas de la conclusión.
En este caso nos encontramos con una regla que es el esquema de un
razonamiento que tiene la forma del modus ponendo ponens. A => B
y A son las premisas y B es la conclusión. Si queremos saber
si un razonamiento es o no válido se tiene que comparar
su forma con la de la regla. Veamos un ejemplo:
Premisa 1: Si
estudio entonces aprobaré el examen
Premisa 2: Estudio
Conclusión: Por lo
tanto aprobaré el examen
Si se abstrae la forma lógica de este argumento obtenemos:
A => B
A____
B
Esta forma, derivada de la ley ((p => q). p) => q, es el modus
ponendo ponens en el que p simboliza "estudio" y q "aprendo" y
que se corresponde con la regla del mismo nombre. El argumento del
ejemplo es válido. Si en vez del argumento anterior hubiésemos
aplicado el método para validar este:
Premisa 1: Si
hay fuego entonces hay oxígeno
Premisa 2: Hay
oxígeno
Conclusión: Por lo tanto hay fuego
Comprobaríamos que el razonamiento no es válido
porque su fórmula lógica es:
((p=>q).q)=>p
que no es una ley lógica y que, en consecuencia, no se corresponde
con la regla del modus ponendo ponens en la que en la segunda premisa
se afirma el antecedente para asi obtener válidamente el
consecuente.
Vamos a considerar otra regla, en este caso derivada del modus
tollendo tolens, en la que negando el consecuente se niega válidamente
el antecedente. El modus tollens tiene la siguiente forma:
((p=>q) . -q) => -p
la regla lógica correspondiente es:
A => B
-B_________
-A
El razonamiento que se validará es el siguiente:
Premisa 1: Si ahorramos
entonces tendremos fondos disponibles
Premisa 2: No
tenemos fondos disponibles
Conclusión: Entonces no ahorramos
El razonamiento es válido porque se corresponde perfectamente
con la regla.
Pues"ahorramos" se simboliza por A y "fondos
disponibles" por
B.
Este método de validación es aplicable a todos aquellos
argumentos cuyas fórmulas lógicas
pueden ser abstraídas. Si dichas formas son leyes de las
que se derivan reglas válidas de
argumentación y los argumentos tienen la misma forma entonces
sera válidos en cualquier
caso.
Se puede comprobar la validez de argumentos no interpretados de
distinto grado de complejidad. Por ejemplo el siguiente:
((-pwq) => -(-r . t)) . (-r.t)) => -(-pwq)
en el que (-pwq) es A y -(-r . t) es B y que tendría la
siguiente estructura metalógica:
A => -B
B____
-A
que es válida ya que se trata del modus tollendo tollens
en el que la negación del consecuente nos permite obtener
válidamente la negación del antecedente. No olvidemos
que doble negación equivale a una afirmación y que
negar -B es afirmar B, como sucede en la segunda premisa del ejemplo. |
[ Arriba ]
ÁRBOLES LÓGICOS
El método de los árboles lógicos es un método
introducido en la lógica a partir de las investigaciones de
Gentzen. Se usa de distintos modos y su propósito es probar
la consistencia o validez de los argumentos. Si se sigue el procedimiento
de Smullyan y Jeffrey se usa un solo árbol y en cada punto
del mismo hay una sóla fórmula. Las reglas básicas
consisten en descomponer las fórmulas que se quiere analizar
en fórmulas más simples y clausurar o cerrar las ramas
del árbol así formado en aquellos casos en que haya
contradicciones. El símbolo usado para indicar que una rama
esta cerrada es una "x". En general bastaría con
que una de las ramas no pueda ser cerrada para que el argumento cuya
consistencia se pretende probar quede validado. Si se sigue a Jefrey
se puede usar algo similar a lo que sería una demostración
por el absurdo. Se trata de probar la consistencia de argumentos
que en caso de ser válidos, al negarse su conclusión
se incurriría en una contradicción, dado que de premisas
verdaderas no se puede obtener conclusión falsa. Para aplicar
el método en cualesquiera de sus dos modalidades se utilizan
una serie de reglas que expresan el funcionamiento de la doble negación,
el condicional, la conjunción y la disyunción inclusiva
y el bicondicional. Reglas:
R1) Doble Negación:
Esta regla indica que se puede derivar válidamente de la doble
negación de una fórmula cualesquiera su afirmación.
R2) Implicación:
A => B |
; |
-(A => B) |
| -AvB |
|
A
-B |
Estas reglas expresan el funcionamiento del condicional. La de
la izquierda nos dice que el condicional puede ser verdadero cuando
su antecedente es falso o su consecuente es verdadero. La de la
derecha nos indica que el condicional es falso cuando su antecedente
es verdadero y su consecuente es falso. Estas reglas autorizan
derivar válidamente de un condicional cualesquiera la disyunción
entre su antecedente negado y su consecuente, y de su negación,
la conjunción de su antecedente con su consecuente negado.
R3) Conjunción:
A.B |
; |
-( A . B) |
A
B |
|
-A v -B |
En estas reglas se convalida la derivación de la conjunción
a partir de la conjunción y, por la ley de De Morgan, la
negación alternativa de la disyunción a partir de
la conjunción negada.
R4) Disyunción:
En estas reglas se convalida la derivación de la disyunción
a partir de si misma y se vuelve a aplicar la ley de De Morgan
para validar la derivación de la doble negación de
la conjunción de la disyunción negada.
R5) Doble implicación:
A |
 |
B |
A
B |
|
-A
-B |
Las fórmulas derivadas como disyunción forman una
horqueta, como si fuesen las ramas de un árbol, y las fórmulas
derivadas como conjunción constituyen una hilera. Cuando
no se niega su conclusión si un argumento es válido
alguna de las ramas queda abierta, es decir que no se detecta una
contradicción remontándola por el tronco hasta su
inicio. Sea el argumento:
Si los alumnos estudian, aprenden
Los alumnos estudian
Por lo tanto aprenden
La fórmula que lo representa es la que se corresponde con
el modus ponendo ponens:
| p => q |
1º premisa |
| p |
2º premisa |
| q |
3º
conclusion |
con la misma se puede formar el árbol:
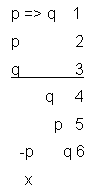
en el que una de las ramas
queda abierta, lo que prueba que el argumento es válido. Si en el mismo argumento negáramos
la conclusión el arbol sería:
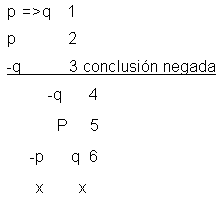
con sus dos
ramas cerradas como consecuencia de haber supuesto que su conclusión
no era
consistente.
Dado el siguiente argumento:
p => q 1º premisa
q => r 2º premisa
p => r 3º conclusión
se puede formar el siguiente árbol negando la conclusión:
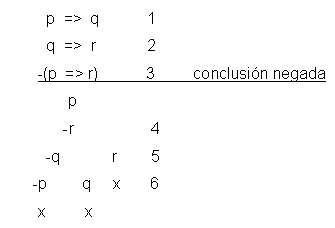
Como se ve, todas
las ramas cierran cuando se comprueba, al remontarlas, que en algún
punto de las mismas hay una fórmula que contradice a una
anterior. En la rama en horqueta de ia izquierda -p y p se contradicen
y q y -q también. En la rama derecha
r es negada por -r. Esto prueba que el argumento en cuestión es válido,
ya que de la
suposición de que no lo era se dio una inconsistencia. |
[ Arriba ]
FALACIAS NO FORMALES
Las falacias son argumentos no válidos. Son de dos tipos:
formales y no formales. Las falacias no formales son múltiples,
y, a mero título de ejemplo, nombraremos un par de ellas.
La falacia de composición, que consiste atribuirle al todo
alguna propiedad de las partes. Las generalizaciones infundadas son
ejemplos típicos, como cuando se asevera cada uno de los miembros
de un equipo es competente y, por ende, el equipo tambien lo es.
La falacia de división, que consiste en atribuirle a las partes
de un todo la misma propiedad que caracteriza al todo. Usando el
ejemplo del equipo, pero a la inversa, se asevera que el equipo es
fuerte y que por lo tanto cada uno de sus integrantes también
lo es.
Una falacia más sutil se da cuando le atribuimos al todo la
propiedad que caracteriza a cada una de sus partes pero que define,
a su vez, a ese todo como conjunto. Por ejemplo, cuando se dice que
el conjunto de los médicos cura. El conjunto de los médicos
no tiene la propiedad que lo define como tal. El conjunto de objetos
cuya propiedad es ser médico no cura. Curan los individuos
cuya profesión es la medicina. El conjunto de objetos cuya
propiedad es ser lapicera no es una lapicera y por lo tanto no sirve
para escribir.
FALACIAS FORMALES
Las falacias formales son argumentos mal hechos
que se derivan de errores en la construcción de esquemas de argumentación
semejantes a las reglas derivadas de leyes lógicas. Dos de
esos esquemas no válidos son de uso comun en el discurso no
científico. Se trata de la falacia de la afirmación
del consecuente en el modus ponendo ponens y de la falacia de negación
del antecedente en el modus tollendo tollens. En el primer caso se
toma como válido el siguiente esquema:
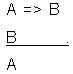
Derivado de la fórmula: ((p => q). q) => q
que no es una ley lógica sino un contingencia. En el segundo
caso se toma como válido el esquema:
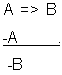
derivado de la fórmula: ((p => q). -p) => -q que no
es una ley sino una contingencia.
También es una falacia el modus ponendo tollens aplicado
a la disyunción inclusiva, pues:
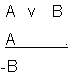
se corresponde con la fórmula: ((p v q). p) => -q
que es una contingencia. |
[ Arriba ]
EQUIVALENCIAS
Todas las conectivas, por
definición, son equivalentes entre
sí. Esto permite sustituir a una conectiva por otra en un
sistema axiomático formalizado de acuerdo a ciertas reglas
previamente establecidas. También es posible reducir cualquier
fórmula a una fórmula elemental en la que las conectivas
sean únicamente la conjunción, la disyunción
y la negación. Esto permite simplificar mucho la estructura
de un lenguaje formalizado porque con ello se puede reducir la cantidad
de conectivas utilizadas. La siguiente lista de equivalencias, algunas
de las cuales ya se han visto en las leyes lógicas, es de
utilidad cuando se busca la simplificación de fórmulas
complejas:
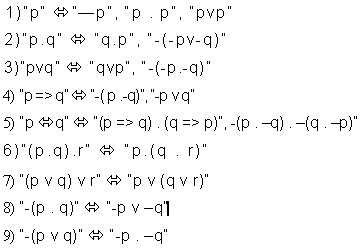
Según la definición de W. Quine dos esquemas lógicos
simbolizados por S y S' son equivalentes si y sólo si no
existe ninguna interpretación que asigne a S y S' distintos
valores de verdad o, dicho de otro modo, si no hay un bicondicional
que tenga por miembros a S y S' y pueda ser falsado.
Usando el método de la asignación de valores se puede
determinar si dos fórmulas son equivalentes entre sí.
Veamos un ejemplo dado por W. Quien:
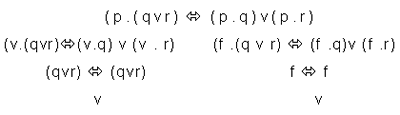
El mismo procedimiento se puede aplicar a otros casos.
FORMAS NORMALES
Todas las conectivas pueden
reducirse a una de ellas. La conjunción
puede representarse por la disyunción y esta por la primera
según las leyes de De Morgan, y así con todas las
demás. No obstante, todas las conectivas son de utilidad.
Sobre todo el condicional y el bicondicional. El primero por la
noción de implicación y el segundo por la de doble
implicación. Pero muchas veces es necesario sustituir dichas
conectivas por sus equivalentes usando la conjunción o la
disyunción. El disponer de estas dos últimas es sumamente
importante cuando se trata de reducir fórmulas con varias
conectivas y con la negación afectando a conjuntos de variables
en vez de afectar a cada una de ellas por separado, a fórmulas
con dos conectivas y con la negación afectando a cada variable
de la misma. La ley de distributividad de la de conjunción
en la disyunción permite transformar:
1°) 'p . (q vrvs)'en '(p . q) v (p . r )v (p v s)'
y a la fórmula:
2°)
'p v ( q . r . s)' en '(p v q). (p v r).
(p v s) '
por la ley de distributividad de la disyunción en la conjunción.
Una definición por equivalencia y la ley de la doble negación
nos autoriza a considerar:
(p.q) 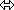 -(-pv-q) -(-pv-q)
Se denominan "formas normales" a las fórmulas del cálculo obtenidas por estos
procedimientos. Hay dos formas normales: la conjuntiva y la disyuntiva.
Una forma normal conjuntiva es una conjunción no negada
de disyunciones no negadas de fórmulas atómicas negadas
o no negadas. Una forma normal disyuntiva es una disyunción
no negada de conjunciones no negadas de fórmulas atómicas
negadas o no negadas. Dado que la negación en toda forma
normal debe afectar únicamente a una variable, es decir
que no puede haber negaciones que afecten a proposiciones moleculares,
debe seguirse un procedimiento adecuado para ubicar a la negación
en el lugar correcto de cada fórmula en la que aparezca.
Este procedimiento se hace de acuerdo a ciertos teoremas y a convenciones
que permiten sustituir unas fórmulas por otras.
La ley de la doble negación permite sustituir: "--p" por "p"; "---p" por "-p";
etc.
Las leyes de De Morgan autorizan a sustituir: "-(p . q)" por "-p
v -q), y -(p v q) por -p . -q,
de modo que la negación afecta directamente a cada variable
atómica.
La propiedad conmutativa , más la asociativa y la distributiva
de la conjunción y la disyunción, que son leyes lógicas,
sirven para transformar cualquier fórmula normada con ".", "v" y "-" como
operadores y sin fórmulas negadas, salvo las atómicas
y sin doble negación, en una forma normal conjuntiva o disyuntiva
de la lógica de enunciados.
La forma normal conjuntiva de la siguiente fórmula (p v
q) => r se obtiene:
1) -(p v q) v r por
la ley de equivalencia del condicional: p=>q =df. –p v
q
2) (-p . -q) v r por
la ley de De Morgan.
3) (-p v r) . (-q v r) por
propiedad distributiva.
La fórmula "(-p v s) . (-q v s)" es la fórmula
normal conjuntiva de "(p v q) => s", que se puede
transformar en la forma normal disyuntiva de la misma fórmula
partiendo de (3)

Las formas normales que permiten
expresar cualquier fórmula
usando la conjunción, la disyunción y la negación
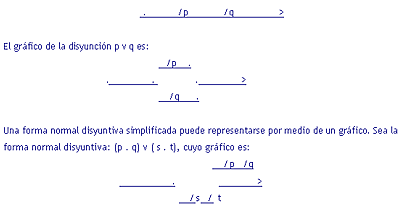
son importantes por su aplicación a los circuitos eléctricos.
W. Quine(1950) señala que C. Shannon en 1938 observó una
estrecha correspondencia entre los esquemas lógicos y los
circuitos. Se comprobó que un circuito cuyo gráfico
eran dos terminales con dos interruptores entre ambos podía
corresponder a una conjunción o a una disyunción
según se tratara de un circuito en serie o en paralelo.
En los primeros, dado que los interruptores están conectados
en serie, la corriente pasa sólo cuando los dosinterruptores
están cerrados, mientras que los segundos, dado que los
interruptores están conectados en paralelo, la corriente
pasa cuando uno u otro esta cerrado. Estas son las funciones
de la conjunción y la disyunción, mientras que la
negación representa la desconexión de un interruptor.
El gráfico de la conjuncion p . q es:
Shannon usó las llamadas álgebras
de Boole y dijo al respecto que " El álgebra de la
lógica de
Boole es un método simbólico para investigar relaciones
lógicas. Los símbolos del álgebra de Boole
admiten dos interpretaciones lógicas. Si los intérpretes
en término de la lógica de clases las variables no
se limitan a los valores 0 y 1. Esta interpretación es conocida
como álgebra de clases. Pero si se acuerda que los términos
son proposiciones, tenemos el cálculo proposicional en las
que las variables se limitan a los valores 0 y 1". A partir
de esto Shannon estableció una serie de analogías
entre el cálculo proposicional y el
cálculo de circuitos, que es lo que posibilita, a partir
de formas normales, obtener el gráfico de circuitos correspondiente.
La siguiente es una tabla de analogías (Garrido-405):

|
[ Arriba ]
CLASES
Las clases (conjuntos, en matemática) son colecciones de objetos
con alguna propiedad en común. Por "propiedad" se
entiende una atribución de cierto tipo que corresponde o no
a elementos individuales. Una propiedad que se atribuye a individuos
puede determinar otra propiedad, ya sea por negación de la
misma o por combinación con otra propiedad. Asi la propiedad "ser
alto" negada se convierte en "no ser alto". La propiedad "ser
sano" combinada con la propiedad "ser persona" se
convierte en la propiedad "ser persona sana". Tanto las
propiedades como su negación (que también son propiedades)
y las propiedades complejas determinan clases de objetos. Estas clases
están constituidas por individuos que son sus elementos. Las
clases no tienen la propiedad que caracteriza a los elementos que
la componen. La clase de las lapiceras no escribe. La clase es una
entidad abstracta.
Hay operaciones entre clases y relaciones entre ellas. Las operaciones
son el
producto o intersección, la suma o unión y la negación
o complemento. Las relaciones son la inclusión y la equivalencia.
Tanto las operaciones como las relaciones son isomorfas con la conjunción,
la disyunción, la negación, el condicional y el bicondicional
de la lógica de enunciados.
CLASES: UNIVERSAL, VACIA, NO VACIA, UNITARIA
La
clase universal, que se puede simbolizar V: definida como la clase
de todos los objetos cuya propiedad es ser idénticos a sí mismos.
La clase no vacía, representada por 1: definida como la
clase que tiene al menos un elemento.
La clase unitaria: definida como la clase que tiene sólo un
elemento. La clase vacía, representada por 0: definida como
la clase de todos los objetos cuya propiedad es no ser idénticos
a sí mismos.
En general las clases son vacías (0) o no vacías (1).
Tanto la clase universal (V) como la clase unitaria son no vacías
(1).
Como con la clase universal considerada en términos absolutos
no se puede operar se ha convenido en considerar "clase universal"(V)
a clases limitadas en cuanto a la propiedad, aunque no siempre en
cuanto a los elementos, a las que se las ha denominado "universo
de discurso", "campo" o "referencial".
Un universo de discurso es un conjunto genérico que abarca
a otros conjuntos, que son subconjuntos del universo en cuestión.
Así, el universo de discurso de los vertebrados es el de los
animales. Los universos de discurso pueden ser más o menos
extensos. La clase de los objetos cuya propiedad es "ser saludable",
es una subclase del campo de los animales o de los seres vivos. Su
complemento: "no ser saludable" no esta constituido
por todo a lo que se puede considerar que no tiene salud, sino
por todos los individuos carentes de salud que pertenecen a alguna
subclases del campo de los seres vivos.
OPERACIONES ENTRE CLASES
El producto o intersección entre clases
equivale a la conjunción
entre proposiciones. Los valores 1 y 0 son equivalentes a los valores
v y f de la lógica de enunciados. Dadas las clases A y B
la intersección tiene la siguiente tabla de valores:

|
[ Arriba ]
RELACIONES ENTRE CLASES
Las relaciones entre clases
son la inclusión y la equivalencia.
Son equiparables al condicional y el bicondicional de la lógica
de proposiciones. La tabla de valores de la inclusión es la
siguiente:
LA INCLUSIÓN ENTRE CLASES
La relación de inclusion es de clase a clase.
Una clase incluida en otra se denomina"subclase" y se
la define como una clase que no tiene los mismos elementos que
la clase
que la incluye. Toda clase se incluye a sí misma, en cuyo
caso se la considera como
subclase impropia, dado que tiene los mismos elementos que la clase
en la que esta
incluida.
La clase universal incluye a todas las clases y se incluye a sí misma.
La clase vacía puede estar incluida en cualquier clase y también
en si misma.
La relación de pertenencia es de elemento a clase, no de clase
a clase.
La lógica de clases esta relacionada con la lógica
de predicados. Los términos de propiedad
son los predicados de enunciados atómicos. Un
enunciado como "Los vertebrados son
animales" expresa una relación de inclusión entre
el sujeto "vertebrados" que se predica de
ciertos individuos x (la clase A) y el predicado "animales" que
se predica también de
individuos x (la clase B) que se puede representar: A C B.
Un razonamiento como el
siguiente:
Todos los matemáticos son lógicos
Todos los calculistas son matemáticos
Luego:
todos los calculistas son lógicos
En la lógica de enunciados se tendría que expresar:
(p . q) -> r. El razonamiento del ejemplo es un razonamiento válido,
por lo tanto si se tuviesen que hacer las tablas de verdad de la
fórmula que debiera representarlo daria una tautología.
Pero la fórmula de la lógica de enunciados es una contingencia.
En la lógica de predicados cada término es interpretado
como una proposición atómica en la que se predica una
propiedad a individuos: Ax, son los x matemáticos, Bx son
los x lógicos, Dx son los x calculistas. Cada una de las proposiciones
está ligada a otras de modo que el razonamiento completo debiera
expresarse: ((A C B) . (D C A)) => (D C B) que daría una
tautología.
Contando con los elementos que nos brinda la lógica de clases
toda las silogística aristotélica puede ser justificada.
Consideremos esto nuevamente: con los cuatro tipos de enunciados
clasificados según la cantidad y la cualidad se pueden construir
razonamientos silogísticos válidos, Estos razonamientos,
como ya se sabe, constan de dos enunciados que sirven de antecedente
a un tercero que es la conclusión. Dado que los tipos de enunciados
son cuatro: A, E, I, O las posibles combinaciones de los mismo de
tres en tres son 256. Pero sólo 19 de ellas son combinaciones
válidas, es decir, combinaciones en las que de las premisas
se derivan válidamente la conclusión. Aristotéles,
y otros lógicos posteriores, agruparon dichas formas válidas
de acuerdo a cuatro figuras o formas genéricas de razonamiento
determinadas por la posición de uno de los términos
que componen los enunciados que hacen de premisa en los mismos.
En el siguiente razonamiento:
Todos los árboles son vegetales
Todos los sauces son árboles
Luego: todos los sauces son vegetales
El término en cuestión es "árboles" y
se lo denomina "término medio" porque se considera
que por su extensión está entre medio de un término
mayor que lo contiene en su extensión dado que alcanza a
más individuos que él (en este caso "vegetales")
y un término menor que esta contenido en el ya que es de
menor extensión al aplicarse a menos individuos (en este
caso "sauces"). La posición del término
medio varía en los distintos tipos de razonamientos posibles
válidos. En el ejemplo dado en la primera premisa es sujeto
y en la segunda predicado. En el siguiente razonamiento:
Todos los profesores son matemáticos
Algunos profesores son lógicos
Luego: algunos lógicos son matemáticos
El término medio es "profesores" y es sujeto en
ambas premisas. Existen dos posibilidades más que permiten
hacer razonamientos válidos con el término medio
como predicado en
ambas premisas y como predicado en la primera y sujeto en la segunda.
Estas cuatro posiciones del término medio posibilitó agrupar
los 19 modos válidos del silogismo en cuatro figuras. Si
se representa al término medio por "M", al término
mayor por "T" y al término menor por "t",
las cuatro figuras del silogismo son:

Todos los modos pueden ser justificados en la lógica de
las clases de acuerdo a los siguientes criterios. Todos los enunciados
equivalen a la negación de sus respectivos contradictorios,
por lo tanto:
A =-0
E =-I
I = -E
0= -A
Todos los enunciados expresan a nivel lingüístico relaciones
entre clases. Por lo tanto los términos de los mismos son
nombres de clases. En general se puede considerar a t, M y T como
nombres genéricos de dichas clases y en tal caso formar
con dichos nombres genéricos todos los modos válidos
de la siguiente manera, teniendo siempre en cuenta la posibilidad
de utilizar los enunciados equivalentes en vez de aquellos a los
que equivalen. En la la F: I= - E y 0= -A, de modo que I= -(t C
-M) o -(t C -T), y 0= -(t C T).

El mismo procedimiento se puede aplicar al
resto de los modos de las otras figuras. Aplicando el cálculo de clases asociado
a los enunciados se obtendría en todos los casos una tautología.
|
[ Arriba ]
|

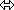 df. -( -p v -q)
df. -( -p v -q)